<目次>
1. はじめに
2. 開発手順
2.1 3円に接する円を求めることは容易ではない
2.2 1点を通り2円に接する円求める手法
2.3 3円に接する円を求める方法
1) 点Oと、円A 半径r1+r0、円B 半径r2+r0とに接する円を求める場合
2) 点O と、円A半径r1+r0、円B 半径r2-r0とに接する円を求める場合
3) 点Oと、円A半径r1-r0、円B 半径r2+r0とに接する円を求める場合
4) 点Oと、円A半径r1-r0、円B 半径r2-r0とに接する円を求める場合
3. おわりに
1. はじめに
以前、1992年から2000年にかけてワイヤカット放電加工機用の二次元CAD/CAMソフトを開発することがあった。CAD/CAMというのはCADで加工したい図形形状を描き、その図形形状を数値制御で動作するNC工作機械で加工するための移動制御プログラム(NCデータ)を作成(CAM)するシステムである。ここで開発したのは銅線(直径0.1~0.2mm)のワイヤで放電しながら金属を加工する装置用の2次元CAD/CAMシステムであった。その開発においては、上下異形状(例えば上部は円、下部は四角)NCデータを作成する機能などの開発に苦慮した。
またCAD機能においては、ある図形に接する円を求める機能 が要求される。形状は滑らかに変化する曲線が好まれる。二つ以上の図形に接する曲線を求める機能(例えば、1点を通り2直線に接する円をもとめる等)についてはとても苦慮したことがある。その一つが3円に接する円を求めることであった。3円に接する一つの円を 中心座標(x,y)と半径rで表現しようとすると、計算途中で二つの式と変数が3個の状態となり求められなくなった。そこで、求めようとする円の中心座標を半径と角度により表現し、角度をあるピッチで探索するようにした。その後、解がありそうな範囲を絞り込み、解を求める手法をとり、解決できた。
本報告は、某企業で現実に生じた問題を解決した考案プロセスを紹介するものである。
2. 開発手順
2.1 3円に接する円を求めることは容易ではない
図1に示すように、3個の円が1)円O、2)円A、3)円B とする。そして、これらの3円に接する円を円Cとした場合、このまま数式を解こうとしても複雑で難解な問題となることがわかる。
ここで計算を簡単にするために、1)円Oをその半径分だけ小さくして恬として扱い、円1及び円2の半径も円Oの半径分だけ小さくすると、1点を通り2円に接する円を求めることとすることができる。これは、図2に示すように赤色の円が求めようとする接円となり、より簡単化できることを理解していただけると考える。
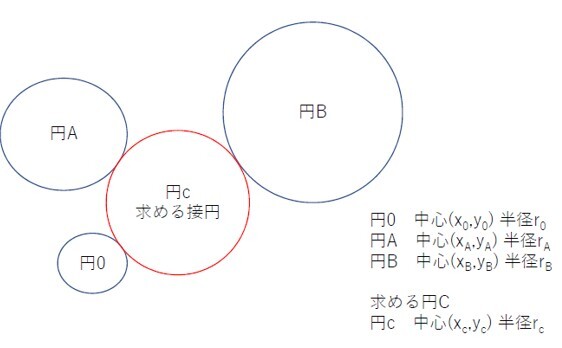
図1 3つの円(円0、円A、円B)に接する円Cの関係
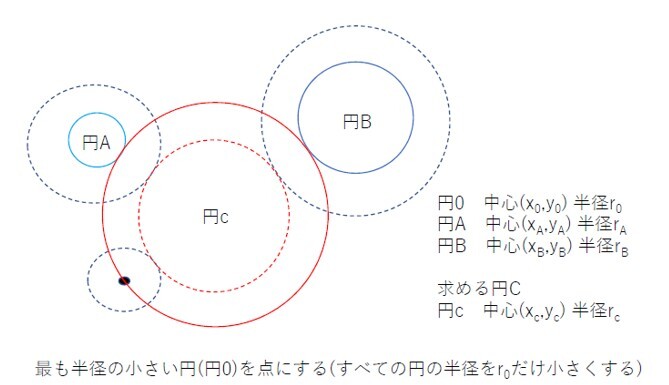
図2 円0を点にして、1点を通り2つの円(円A、円B)に接する円Cの関係
さらに図3に示すように、点0(円0の中心)が原点になるように移動、二つの円Aおよび円B も中心座標を移動させ、それぞれ円1、円2 とした。
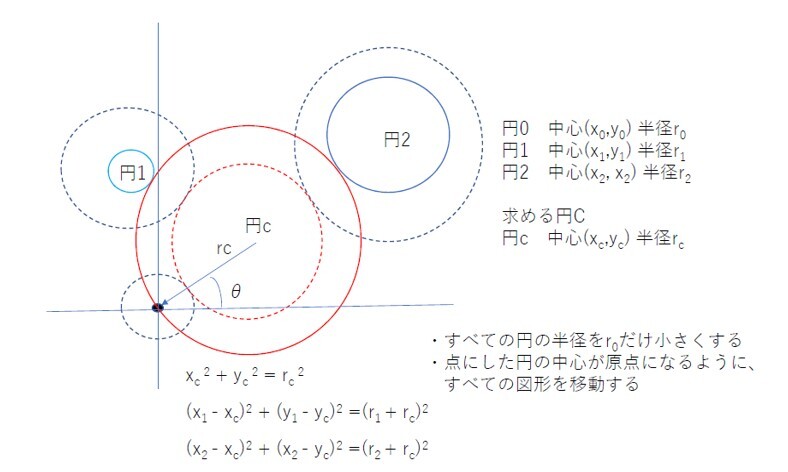
図3 円0の中心点が原点になるように全体を移動して、接円Cの問題を簡素化する
そして、求めようとする円Cとの関係式は以下のようになる。ここで示す②③及び④の式は円の中心座標と半径による式である。
xc2 + yc2 = rc2 -------- ①
(x-x1)2+(y-y1)2 = r12 -------- ②
(x-x2)2+(y-y2)2 = r22 -------- ③
(x-xc)2+(y-yc)2 = rc2 -------- ④
ここで円C はそれぞれ3円に接するので 以下の3式が導出できる。式⑤は原点から円Cの中心位までの距離、式⑥は円1と円Cの中心位置の距離、式⑦は円2と円Cの中心位置の距離との関係を示す式である。
xc2 + yc2 = (rc±r0)2 ---- ⑤
(xc-x1)2+(yc-y1)2 = (rc±r1)2 ---- ⑥
(xc-x2)2+(yc-y2)2 = (rc±r2)2 ---- ⑦
ここで半径の数値に±があるのは内接または外接に対応する。そして、変数は円Cの中心座標と半径の3個で式も3式あるので解が求められそうであるが困難である。しかし、一つの円を点としてとらえ、その半径分の数値を他の円の半径に加算または減算することで計算を簡略化できそうだと考えた。
2.2 1点を通り2円に接する円を求 める手法
1点は点Oとする。また二つの円をそれぞれ円A、円Bとする。ここで計算を簡単にするために、点Oを原点に移動させ、二つの円A(添え字番号1)および円B (添え字番号2)も中心座標を移動させ、求めようとする円C(添え字C)とすると以下の式が成り立つ。
(x-xc)2+ (y-yc)2 =rc2 ---⑧
(x1-xc)2+(y1-yc)2 =(r1±rc)2 ---⑨
(x2-xc)2+(y2-yc)2 =(r2±rc)2 ---➉
⑨および➉式において±があるのは、内接または外接の場合があるからである。
⑧式は原点を通るので
xc2 + yc2 = rc2
が成り立つ。また⑨及び➉式より
x12 +y12 -r12 = 2(x1・xc +y1・yc ±r1・rc)
x22
+y22 -r22 = 2(x2・xc +y2・yc ±r2・rc)
の二式が求められるが、変数は円Cの中心座標と半径の3個があるのに対し、式は二つしかないので容易に求めることはできない。
そこで、円Cの中心座標は原点位置からの半径 と角度で求めることとして考え
xc = rc cosθ、yc = rc sinθ
とすると
x12 +y12 -r12 = 2rc(x1cosθ+y1sinθ±r1)
x22 +y22 -r22 = 2rc(x2cosθ+y2sinθ±r2)
となる。また、
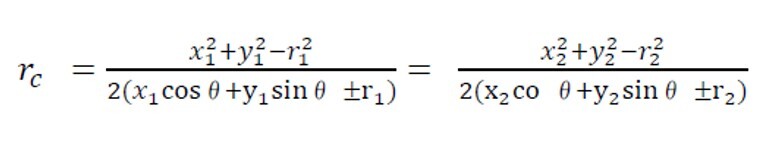
となり、さらに
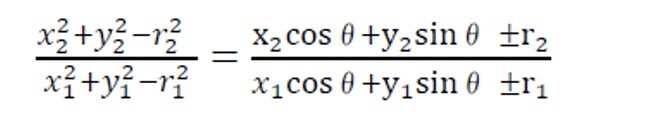
とすることができる。
ここで
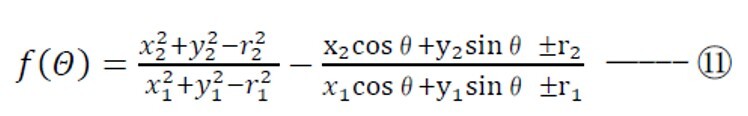
とする。ここで f(Θ)=0 となるθを求めることで求めようとする接円の中心座標と半径を求めることができる。そして、以下の4つのそれぞれの場合において、θを0~2πの間をある一定ピッチで求めてみることとした。
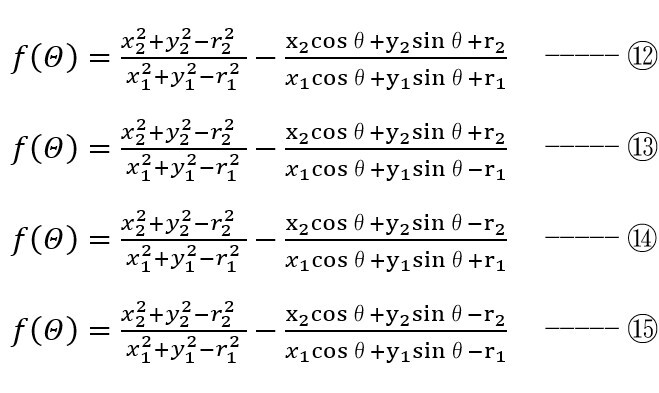
また、具体的に、点(5,5)、二つの円を、円A中心(50,50)半径r=50と、円B中心(-60,-10)半径=40として求めてみた。図4に図形の状況を示す。
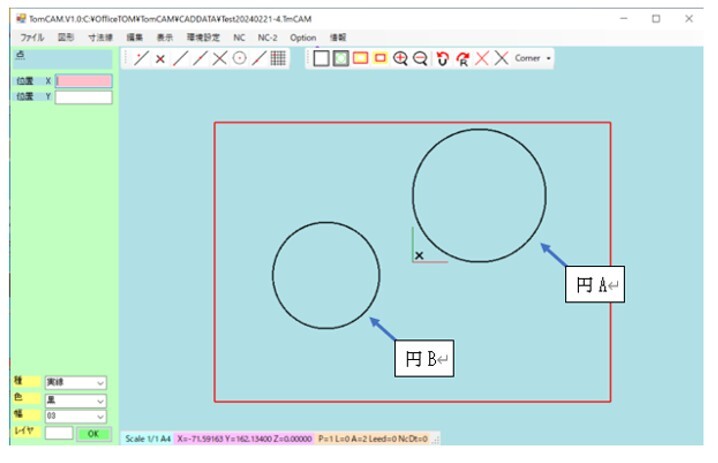
図4 1点(5,5)と2個の円(中心(50,50)半径r=50と中心(-60,-10)半径=40)を設定
プログラムは θを0~2*PI(6.28)までの間をピッチ0.2で f(θ)の数値を求めた。
まず円A および円B に対して外接する式⑫の場合の結果を図5に示す。
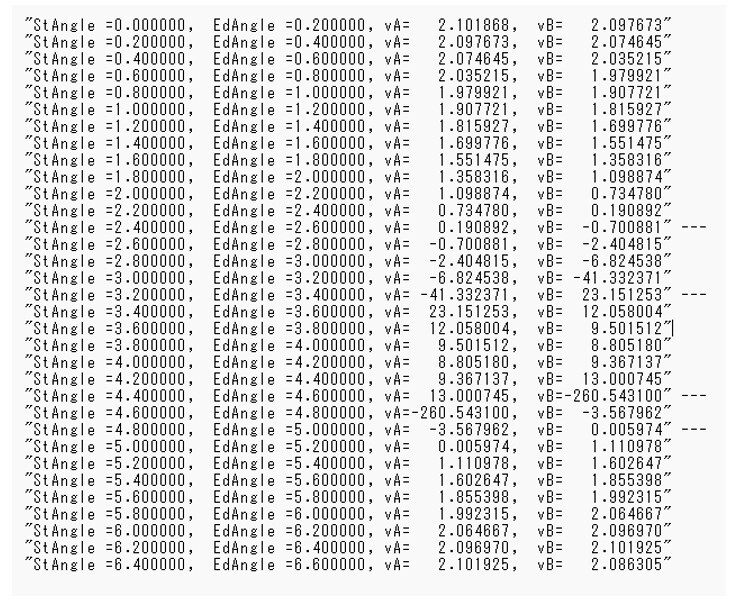
図5 円A及びBにおいて外接となる場合のf(θ)の計算結果
この時θの値がStAngleのときのf(θ)の値Vaと、EdAngle のときのf(θ)の値Vbが正から負へ、または負から正へ逆転している区間において解があることになる。図において 右端に「---」を付加した部分である。このデータのStAngle と vA で示す値をグラフにした図を図6に示す。
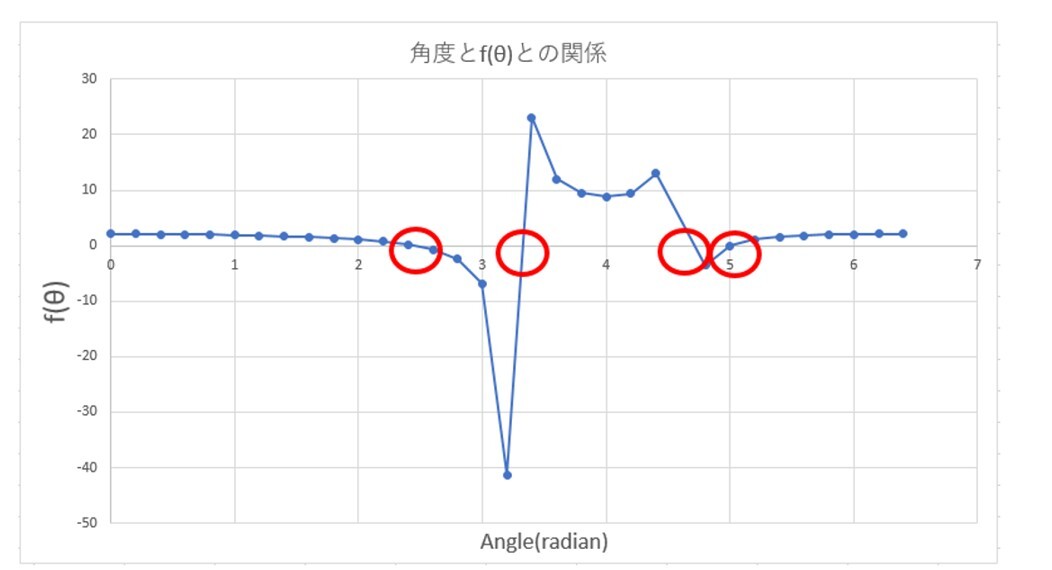
図6 図5で示した角度θと関数f(θ)(vAで示した数値) のグラフ
この図6のグラフでは、角度4.6(radian)のf(θ)= -260.5431のデータはグラフがわかりにくくなるため削除している。この図からわかるように赤丸で示した4か所の位置は、f(θ)の値が正から負になる区間、または負から正になる区間であり求める解がある。これらの区間で挟み込み方式で正解値を求めることとした。
このようにして、円A及び円Bに対して 外接と外接、内接と外接、外接と内接、内接と内接のそれぞれの場合の角度の範囲を求めた(図7参照)。

図7 各条件において角度の正解値が求められる区間のリスト
ここで、式⑫の場合におけるStAngle=2.45, EdAngle=2.50 及びStAngle=3.25, EdAngle=3.30の区間において、挟み込み方式により極致を求める。ここで、挟み込み方式について具体的に説明する。まず、図8-1に示すStAngle=2.45, EdAngle=2.50の区間内に解があるはずなので、中間値Angle=2.475でのf(θ)=-0.088202を求める。この時f(θ)=0となるのはStAngle=2.45とAngle=2.475の区間内に存在するはずなので、EdAngle=2.475として、さらにStAngle=2.45, EdAngle=2.475の中間値Angle=2.4625とf(θ)=-0.037884を求める。
この操作を繰り返し、vA=vBとなるθを求めることとなる。その計算処理過程を図8-1には示す。この処理では収束したことがわかる。しかし、StAngle=3.25, EdAngle=3.30の区間においてはvAとvBの値は一致することなく、大きく離れてしまい発散してしまった。この場合は解が求められなかったこととなる。
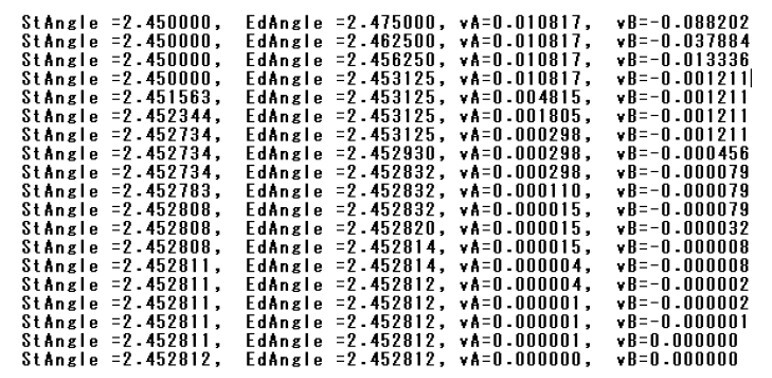
図8-1 StAngle=2.45, EdAngle=2.50の区間において求められた結果

図8-2 StAngle=3.25, EdAngle=3.30の区間において発散した結果
これらの各区間において角度の正解値と円の中心座標と半径の結果を図9-1に示す。

図9-1 求められた角度範囲において挟み込み手法で確定した結果
この結果において、8個の解が求められたが、中心座標と半径の数値が重複しているものがあり、整理すると図9-2に示す結果となる。
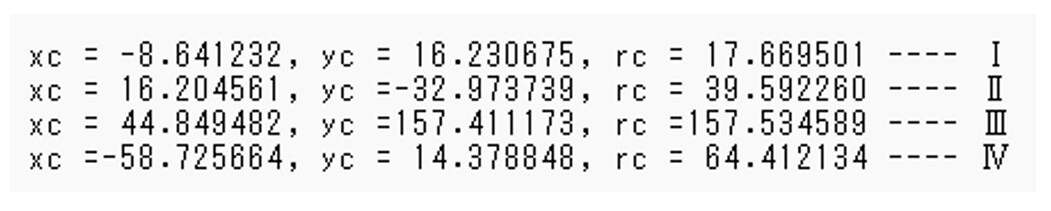
図9-2 求められた角度範囲において挟み込み手法で確定した結果
それぞれの領域において解となる数値を求めると4つの解を得ることができた(図9参照)。また、求められた解によって作成された円を図10に示す。
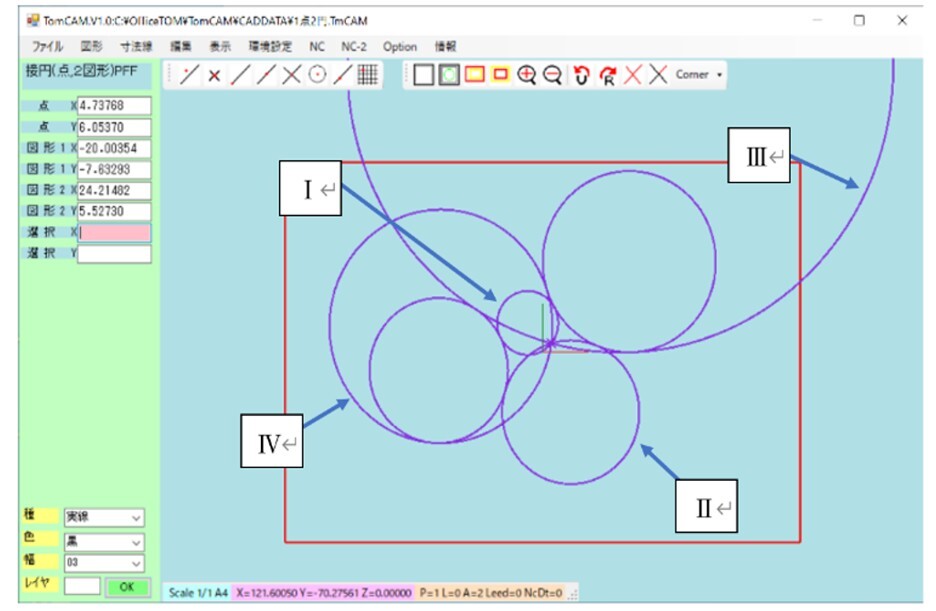
図10 求められた解による4つの接円
この手法を利用して、3円に接する円を求めることとした。
2.3 3円に接する円を求める方法
ここで、3個の円を円Oの中心座標(5,5)半径5、円Aの中心座標(50,50)半径50、円Bの中心座標(-60,-10)半径40とする。そして、円Oの半径を「0」にして、円Aの半径を円Oの半径分だけ加算・減算、円Bの半径を円Oの半径分だけ加算・減算、として解いてみることとした。
・点Oを通り、円A 半径を円の半径分だけ加算、円B 半径を円の半径分だけ加算とに接する円を求める。具体例として、以下の手順で求める。
1) 点Oと、円A 半径r1+r0、円B 半径r2+r0とに接する円を求める場合
点O(5,5)、円Aを中心(50,50)、半径55(50+5)、円B を中心(-60,-10)、半径45(40+5)に接する円を求める。このとき 以下の4つの解が求められる(図11参照)。

図11 1)の場合での1点を通り2円に接する場合での解
これらの4つの解のうち、点Oを円Oに戻し、円A中心座標(50,50)半径50、円中心座標(-60,-10)半径40の二つの円に接する円の解となるのは、Ⅰ及びⅡ の解である。図12において、円Aおよび円Bの半径は「5」だけ大きくなっており、この分だけ小さくなり、求められた4つの接円が半径を「5」だけ大きくした場合に、円Aおよび円Bに接する円はⅠ及びⅡ の接円のみであることがわかる。結果として図13に示す解が求められる。その解として求められた円を図13-1の赤色の円で示す。
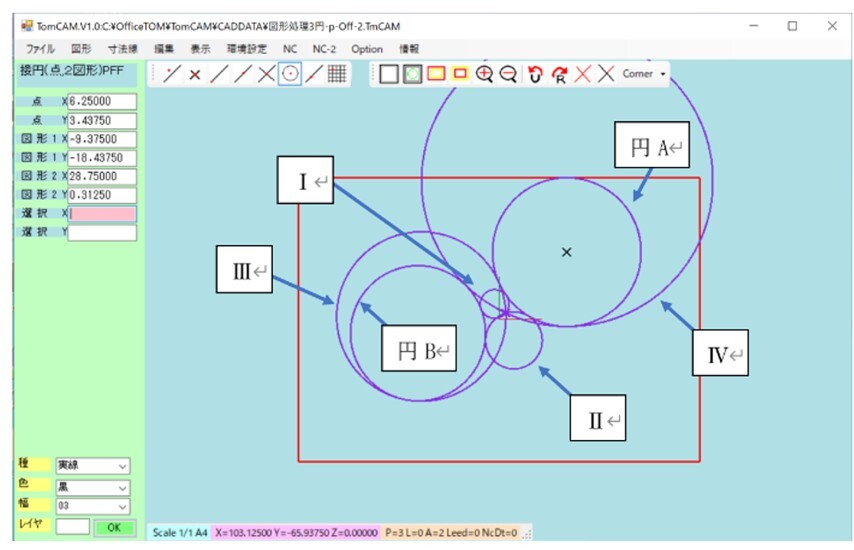
図12 1)の場合での1点を通り2円に接する場合での得られた接円

図13-1 1)の条件で求められた解
これは円Aと解となる円Cとの中心間距離と(rc±r1)が等しく、かつ円Bと解となる円Cとの中心間距離と(rc±r1)が等しい場合である。
同様にして、以下のようにして他の接円も求められる。
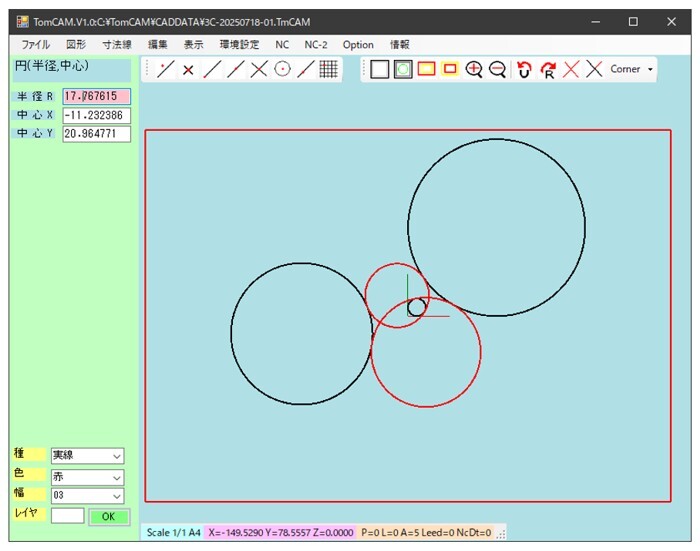
図13-2 1)の条件で得られた解の円の図形(赤色)
2) 点O と、円A半径r1+r0、円B 半径r2-r0とに接する円を求める場合
1)の場合と同様に、点O(5,5)、円Aを中心(50,50)、半径55(50+5)、円B を中心(-60,-10)、半径35(40-5)に接する円を求める。1)と同様にして4つの解が得られ、得られた円の中心と円Aおよび円Bとの中心間距離との関係を確認して、図14-1に示すように二つの解を得ることができた。また、求められた解による円を図14-2に示す。

図14-1 2)の条件で得られた解
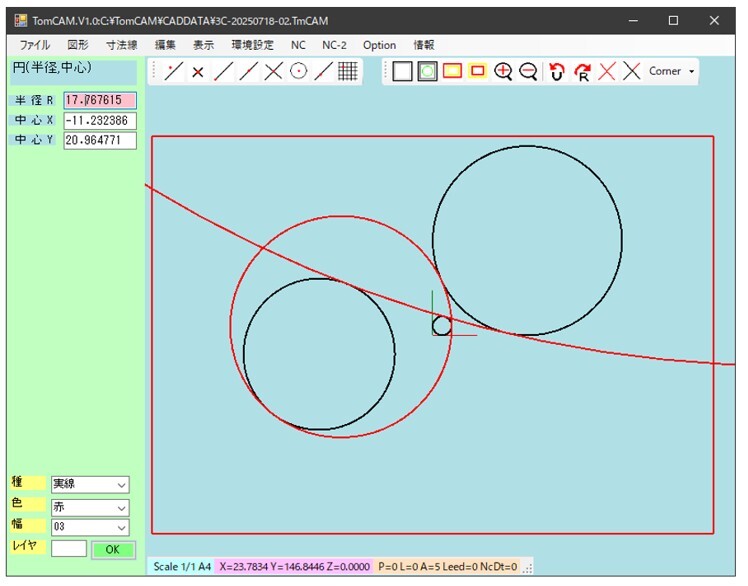
図14-2 2)の条件で得られた解の円の図形(赤色)
3) 点Oと、円A半径r1-r0、円B 半径r2+r0とに接する円を求める場合
同様に点O(5,5)、円Aを中心(50,50)、半径45(50-5)、円B を中心(-60,-10)、半径45(40+5)に接する円を求める。やはり1)と同様に4つの解が得られ、得られた円の中心と円Aおよび円Bとの中心間距離との関係を確認して、図15-1に示すように二つの解を得ることができた。また、求められた解による円を図15-2に示す。
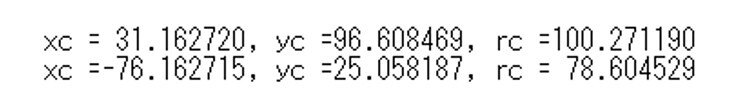
図15-1 3)の条件で得られた解
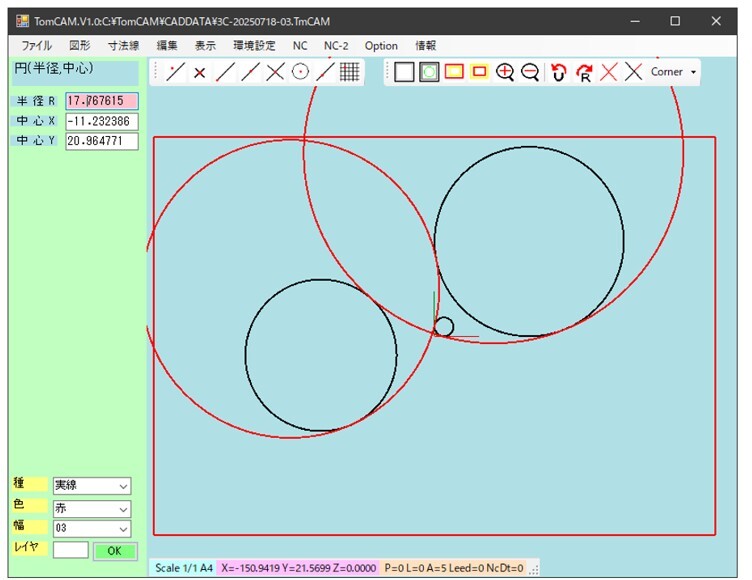
図15-2 3)の条件で得られた解の円の図形(赤色)
4) 点Oと、円A半径r1-r0、円B 半径r2-r0とに接する円を求める場合
同様に点O(5,5)、円Aを中心(50,50)、半径45(50-5)、円B を中心(-60,-10)、半径35(40-5)に接する円を求める。やはり1)と同様に4つの解が得られ、得られた円の中心と円Aおよび円Bとの中心間距離との関係を確認して、図16-1に示すように二つの解を得ることができた。また、求められた解による円を図16-2に示す。
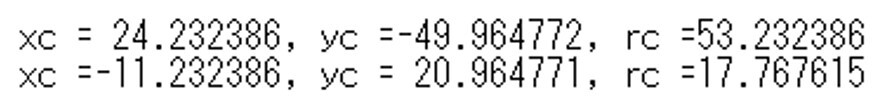
図16-1 4)の条件で得られた解
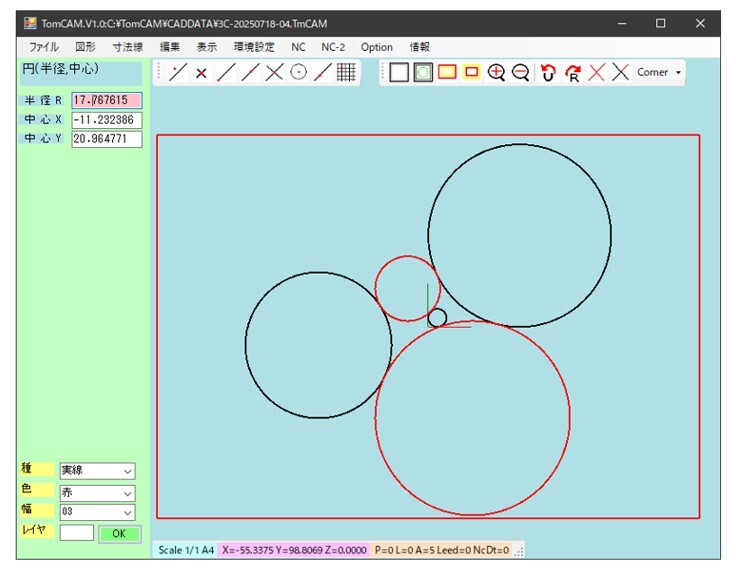
図16-2 4)の条件で得られた解の円の図形(赤色)
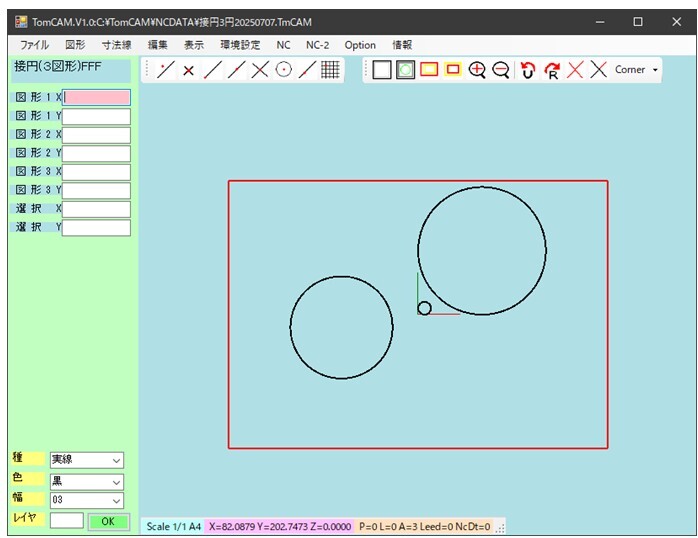
図17-1 設定された3個の円(左)
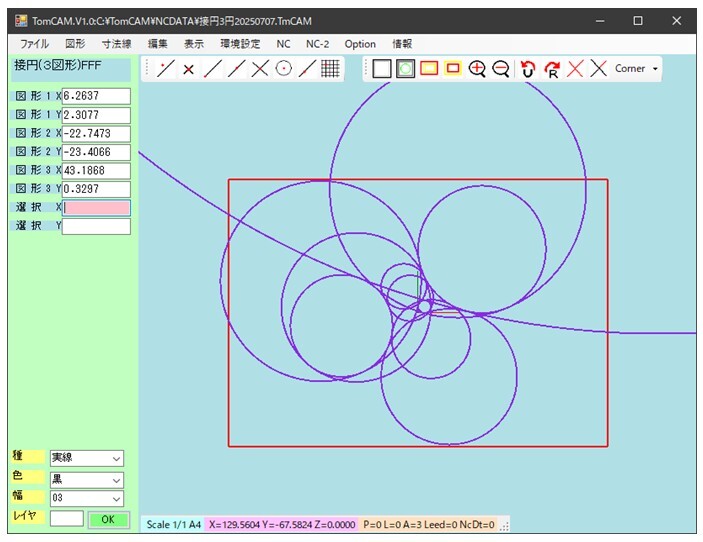
図17-2 3個の円に接する求められた8個の円
以上の手法をプログラムして以下のように求められるようになった。図17に接円の図を示す。
この図を描いているソフトは自作の2次元CAD/CAMソフトであり、図17-1で設定された3個の円に接する円をもとる表示しているのが図17-2に示されている。ここで示されている8個の円のいずれかを指定すると、その円のみが選択されて表示されるようにした。8個の接円のうち一つの円を選択した結果を図18に示す。
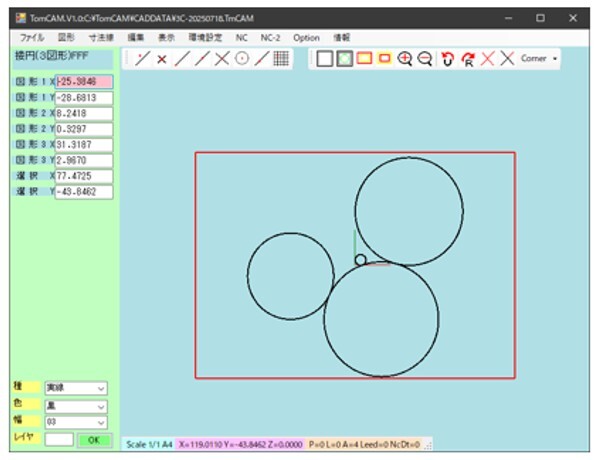
図18 表示された8個の接円のうち1個の円を選択した結果
3. おわりに
3円に接する円を求めようとしたとき、意外に容易に解くことはできなかった。いろいろと試行錯誤の結果、1点を通り2円に接する円を求めることで解決できることに気づき取り組んだ。
また、半径と角度の関係で変数を二つに絞り込んで解を求める手法において、角度のビッチをあまり大きくとると、その狭いピッチ間に二つの解が存在する場合において、一つの解しか見つからない場合があることにも気づいた。当初、1点を通り2円に接する円を求める際に、ピッチを0.2ラジアンで求められていたが、3円に接する円を求める際には、7個の解しか求められなくなっていた。そして、データを詳細に見ていき、ピッチを0.05ピッチにすることで解が求められた。解が存在する範囲が求められたら、その範囲内で挟み込みの手法でもとめることができた。手法としては面白いプログラムとなったと考える。
なお、本手法は2次元CAD/CAMソフト開発で生じた問題を解決する際に個人的に考案した方法であり、あくまで個人見解であることを申し添える。同種の問題解決の一助になれば幸甚である。
<参考文献>
1) 金城俊哉:VisualC#2013 パーフェクトマスター,株式会社秀和システム,2013年12月23日第1版
2) 外山真也 : パソコンCAD&CAM ,海文堂出版( 初版 1993年3月25日)

【執筆者】
外山技術士事務所
代表 外山 真也
技術士(情報工学部門)、博士(工学)
(日本技術士会九州本部/宮崎支部幹事)
【専門事項】
宮崎県工業技術センターにて研究開発に36年間従事、主にCAD/CAM関連の研究開発に従事。C#言語によるソフト開発などを得意とする。現在、宮崎大学工学部などで非常勤講師を務める。※本記事のご利用にあたって
本記事の内容は執筆者個人の見解に基づくものであり、日本技術士会の公式見解ではありません。また、記事の内容は執筆時点の情報に基づいています。ご利用者様自身の判断と責任において、ご活用頂くようお願いいたします。











